Segunda Ley de Newton

Hace muchos años, Newton encontró que había una relación entre la fuerza (F) que se aplicaba a un cuerpo que tenía una determinada masa (m), obteniéndose una aceleración (a), como resultado de dicha fuerza.

Supongamos que podemos razonar de la misma manera que lo hizo el físico hace mucho tiempo, tal vez podamos encontrar, de acuerdo a nuestra experiencia las ecuaciones que escribió Isaac Newton en su libro "Principios Matemáticos de la Filosofía Natural" en el año 1687.-

Para ello, vamos a analizar el siguiente gráfico

Que conclusiones puede Ud. sacar del mismo? Suponga que la fuerza P2 es el doble de P1.-

Si ya lo hizo, mire el siguiente grafico

Con estos datos, podemos establecer que sucedería si quisiéramos relacionar las tres magnitudes citadas en una ecuación que describa la interacción entre ellas.

Tenemos 3 posibilidades, para combinar la masa, la fuerza y la aceleración:

1 -    a=F.m

2 -    F=m.a

3 -    m=F.a

Cual de ellas le parece a Ud. que cumple con lo que se manifiesta en los gráficos?

Debe justificar su respuesta con una explicación detallada de su elección, recuerde que debe analizar cada una de ellas por separado.-

A construir usando el Principio de acción y reacción

Aprovechando lo aprendido en el principio de acción y reacción, vamos a construir algunos prototipos.
A cada alumno se le asignará un tema en clase.

Los temas para construir son:

Tema 1

Construir un auto cuya propulsión sea mediante el principio de acción y reacción, utilizando aire a presión para lograrlo.-
El auto de Vapor fue una máquina construida por Newton en el año 1670. Una simple caldera montada sobre cuatro ruedas, la cual se desplazaba debido al principio de acción y reacción. UD. DEBERÁ REEMPLAZAR EL VAPOR, POR AIRE A PRESIÓN.-

Tema 2

Construir un barco cuya propulsión sea mediante el principio de acción y reacción, utilizando AIRE A PRESIÓN para lograrlo.-

Tema 3

Construir una eolípila de Herón, considerada como la primera máquina a vapor en el siglo I por Herón de Alejandría.-
La eolípila es un curioso mecanismo que consiste en una esfera hueca que rota sobre su eje a la que se adaptan dos tubos curvos. Se llenaba de agua y se ponía al fuego consiguiendo así expulsar vapor por los dos tubos laterales lo que hacía girar de forma rápida el mecanismo. UD. DEBERÁ REEMPLAZAR EL VAPOR, POR AIRE A PRESIÓN,-. 

Recuerden que los vehículos deben ser construidos por Uds. Deberán optimizar el diseño y los materiales usados, para lograr el éxito en el proyecto. Los vehículos deberán desplazarse o girar, según corresponda, para lograr la aprobación del mismo, es decir, el auto deberá avanzar sobre el suelo, el barco sobre una superficie con agua y la eolípila girar sobre su eje. 

Para almacenar el aire a presión deberá utilizar una botella plástica pequeña y adosarle una válvula que permita almacenar el aire de un inflador de bicicletas. Al salir el aire a presión podremos observar como se cumple el principio de acción y reacción. No podrá usar globos, sino botellas plásticas.

En todos los casos, deben trabajar con las medidas de seguridad adecuadas y siempre con antiparras para proteger la vista de objetos pequeños que pueden salir volando. Sin los elementos de seguridad adecuados, no podrán presentar los trabajos y serán calificados como trabajos no presentados, calificados con una mala nota.

Usen la imaginación para realizar la construcción y la forma en que debe usar la propulsión solicitada en cada tema. Recuerden que, en todos los casos, el movimiento deberá estar basado en el principio de acción y reacción. No se aceptarán prototipos que usen otro principio para moverse.-

Buena suerte a todos!!!!!!

Tercera ley de Newton

Ahora vamos a estudiar la tercera ley de Newton, también llamado Principio de Acción y Reacción.

El mismo establece, en primer lugar, que, las fuerzas existen siempre por pares: dado que son interacciones entre cuerpos, ambos ejercen una influencia el uno sobre el otro. No tiene sentido pensar en un cuerpo como originador de la fuerza y el otro como su receptor — ambos son, a la vez, originadores y receptores. Por tanto, no hay una fuerza sobre un cuerpo, sino dos fuerzas, una sobre cada uno de los dos cuerpos.

Aunque creo que es algo bastante intuitivo, tal vez una analogía económica les  ayude a asimilarlo mejor. Supongamos que el estado de movimiento en mecánica es el estado económico de una persona, y que las fuerzas –las modificaciones de ese estado– son ganancias y pérdidas de dinero. Toda ganancia o pérdida, de acuerdo con el tercer principio, no es algo que le sucede a un individuo aislado, sino que es una interacción entre individuos. Es decir, si ganas dinero, alguien te lo ha dado, y si lo pierdes, alguien te lo ha quitado. Los cambios monetarios son siempre interacciones entre dos individuos.
Esto significa que no es posible para un cuerpo modificar su estado de movimiento sin interaccionar con alguien más y, por tanto, modificar el estado de movimiento del otro.-

En segundo lugar, las fuerzas que aparecen sobre ambos cuerpos son de sentidos contrarios. Esto sigue siendo bastante intuitivo, porque lo llevamos notando toda nuestra vida, pero veamos un ejemplo concreto.

Imagina que tú y un amigo están sobre una pista de hielo perfectamente lisa, de pie el uno frente al otro, y en un momento dado pegas un empujón a tu amigo para alejarlo de ti. De acuerdo con el tercer principio, no tiene sentido decir simplemente que tú empujas a tu amigo en una dirección: el empujón se convierte en una interacción entre ambos en la que los dos sufren las consecuencias. Efectivamente, tu amigo empieza a moverse en una dirección, pero tú también sufres un empujón idéntico al suyo en sentido opuesto, y te alejas también del punto en el que te encontrabas

El tercer principio se pone de manifiesto, de hecho, constantemente en nuestras vidas, y seguro que has notado alguna de estas cosas:

• Cuando estás en un bote junto a la orilla y te bajas del bote, éste se aleja de la orilla y puedes incluso caerte al agua si no eres lo suficientemente hábil.
• Cuando disparas un arma y la bala sale disparada hacia delante, el arma a su vez sale disparada hacia atrás con retroceso.
• Cuando saltas hacia arriba en un bote, el mismo se hunde un poco más en el agua justo en el momento del salto.

Hay una multitud de ejemplos obvios, pero si has comprendido la parte evidente de la cuestión, me gustaría pararme en los menos obvios. Si recuerdas la primera consecuencia del principio, no es posible empujar sobre uno mismo: las fuerzas son interacciones. Así, si estás de pie y en reposo sobre el suelo, no es posible modificar ese estado sin interaccionar con alguien. ¡No puedes siquiera andar tú solo!

Lo mismo sucede en cualquier otra situación: si estás flotando en el agua y quieres empezar a moverte, no puedes hacerlo tú solo. Si estás en el aire y quieres volar, no puedes hacerlo tú solo. Podríamos decir que éstas son las “malas noticias” del tercer principio: tú solo no vas a ninguna parte. Sin embargo, evidentemente, tú caminas todos los días, y seguramente alguna vez has nadado o has volado en algún vehículo, con lo que es posible hacerlo utilizando el tercer principio. ¿Cómo sucede esto?

Cuando quieres caminar, de acuerdo con el tercer principio, debes ejercer una fuerza sobre alguna otra cosa hacia atrás. Esa “alguna otra cosa”, en la inmensa mayoría de las ocasiones, es simplemente el suelo: lo empujas hacia atrás con los pies y, como consecuencia del tercer principio, tú sales impulsado hacia delante, en sentido contrario. Caminar es empujar el suelo hacia atrás.-

Pero ¿qué es nadar? ¡Empujar el agua hacia atrás, naturalmente! Cuando mueves los brazos y las manos al nadar, piensa en lo que estás haciendo: estás tomando agua, cuanta más agua mejor, con los brazos, y empujándola hacia atrás. Como consecuencia de esta interacción, el agua te impulsa a ti hacia delante. Lo mismo haces con las piernas y los pies, por supuesto. Y volar es, desde luego, la misma cosa: empujar el aire en una dirección para sufrir una fuerza opuesta. Así vuelan un pájaro, un avión o un helicóptero.

Ahora, pregunto, y tendrán que responder en su carpeta:

¿Como es posible que vuele una cañita voladora? Explique el resultado utilizando el principio de acción y reacción. Realice un grafico y en el mismo grafique las fuerzas que intervienen.-

¿Porqué es tan difícil caminar sobre una pista de hielo con zapatos o zapatillas? Como se puede "mejorar" el calzado para poder hacerlo? Grafique y explique su propuesta.

Enumeren 2 ejemplos, distintos a los citados arriba, de situaciones de la vida real en la que ustedes consideren la analogía de la tercera ley de Newton.-

Trabajo Práctico - Principio de Inercia

Para el trabajo práctico sobre el principio de inercia, necesitarán los siguentes elementos: 

3 monedas de la misma denominación

4 tuercas Pequeñas 

1 trozo de lienzo ecologico - 50cm x 50cm 

1 botella plástica de boca ancha (jugo citric pequeño) 

1 tira de papel de 2cm x 25cm 

1 lata de picadillo o atún vacia 

1 regla plástica de 20cm 

 Procederemos de la siguiente manera

 a) Tomar la lata de atún vacía, colocar la tira de papel en la boca de la misma y sobre el borde y el papel, una moneda en equilibrio. Retirar la tira de papel en forma lenta y luego rapidamente. Observar que sucedió en un caso y luego en otro y sacar las conclusiones correspondientes.-

 b) Colocar las tres monedas apiladas y, utilizando la regla plástica, retirar la moneda de abajo sin mover las monedas superiores.-

c) Colocar la regla en la boca de la botella y sobre ella las tuercas apiladas. Retirar la regla lentamente y luego rápidamente. Observar que sucedió en un caso y luego en otro y sacar las conclusiones correspondientes.-

d) Colocar el lienzo sobre una superficie lisa y sobre el mismo colocar la lata, las monedas y las tuercas apiladas. Retirar el lienzo lentamente y luego rápidamente. Observar que sucedió en un caso y luego en otro y sacar las conclusiones correspondientes.-

Una vez concluidas las tareas, realizar un informe en su carpeta, que será presentado ante el docente, en la fecha establecida por el mismo. Recuerde que su informe deberá ser completo, al principio, deberá consignar el listado de materiales, luego una descripción de las consignas, descripción grafica y textual de las tareas realizadas para llevar a cabo las mismas, con sus respectivas conclusiones y/o inconvenientes con los cuales haya atravesado para cumplir con las consignas.-

Buena suerte!!!!!

Relacion entre inercia y masa

Habíamos visto que la inercia es la propiedad de los cuerpos con MASA de resistirse a cambiar su estado de reposo o movimiento. Newton relacionó el concepto de inercia con la masa de un cuerpo y definió la misma como una "medida cuantitativa de la inercia".
Es decir, a mayor masa de un cuerpo mayor inercia. Mas difícil será detener un cuerpo con mayor masa en movimiento y también será mas difícil ponerlo en movimiento cuando está en reposo. Observemos nuestro entorno y tratemos de encontrar 3 ejemplos en donde se observe la relación directa entre inercia y masa. Compare en cada ejemplo, como sería el mismo si la masa aumenta o disminuye y relacione cada uno con su inercia o resistencia al cambio.-
Graficar y explicar los mismos.-
Deberá Ud. realizar su trabajo en un documento realizado en su carpeta, que se entregará en clases, donde grafique (puede  usar gráficos predeterminados de Internet) y explique los citados ejemplos, siempre relacionados entre inercia y masa. Recuerde que los graficos solo pueden ser copiados, la explicación de los ejemplos será producción individual. El mismo deberá tener su nombre y apellido, curso y división y será presentado en la fecha que lo estipule el docente.-
Mucha suerte.....

Principio de Inercia - Primera ley de Newton

El hombre primitivo, observo con sorpresa que, al arrojar una piedra, ésta seguía moviéndose, sin que nada la impulsara. Durante muchos siglos, nadie pudo explicar con precisión porqué sucedía esto. El hombre moderno se sorprende al saber que, una vez colocados en órbita, los satélites artificiales, continúan girando alrededor de la Tierra. Estos hechos, aparentemente diferentes, obedecen sin embargo al mismo principio de  Física, el de la inercia.

Teniendo en cuenta estos sucesos, te pregunto ¿Que será la famosa Inercia?

Trata de contestar con tus propias palabras y sin espiar mas abajo, a esta pregunta.

Te ayudo................

1- Será una fuerza?

2- Será magia?

3- Será una propiedad natural?

4- Será consecuencia de que la Tierra gira alrededor de su eje?

Te ayudo con algunas imágenes





Ahora veremos si tu respuesta fue correcta.

Resumen en la carpeta.

🔽 

Principio de Inercia

La inercia es la propiedad que tienen los cuerpos de permanecer en su estado de reposo o movimiento, mientras no se le aplique sobre ellos alguna fuerza, o la resistencia que opone la materia al modificar su estado de reposo o movimiento. Como consecuencia un cuerpo conserva su estado de reposo o movimiento si no hay una fuerza actuando sobre él. De ser así el cuerpo dejara su estado original y tomara uno nuevo.En física se dice que un sistema tiene más inercia cuando resulta más difícil lograr un cambio en el estado físico del mismo.
Es decir, los cuerpos quietos permanecen quietos a menos que se les aplique alguna fuerza para que comiencen a moverse. Los cuerpos en movimiento permanecen en movimiento a menos que se les aplique alguna fuerza para detenerlos. El principio de inercia es tan simple como decir que para cambiar la velocidad de un cuerpo es necesario aplicarle una fuerza, hacerle algo, interactuar con él. De este modo, si un cuerpo se está moviendo con cierta rapidez en determinada dirección, seguirá en esa dirección y con la misma rapidez a menos que lo perturbemos. Los cuerpos no cambian su velocidad (dirección y rapidez) si no reciben alguna fuerza.

Por mas que no pensemos diariamente sobre la inercia, esta, como la atracción gravitatoria y otras tantas características que estudiamos en física, te acompañan adonde tú vayas. Por ejemplo, no puedes arrancar tan rápidamente como quisieras al comenzar a correr; tampoco puedes detenerte de golpe. Tu cuerpo tiene inercia!. Es necesario aplicarle una fuerza para que comience a moverse desde un estado de reposo. También tienes que aplicar una fuerza para detenerte, ya que si no, tu cuerpo seguiría con la misma rapidez y en la misma dirección . Si vienes corriendo alrededor de la manzana te costará bastante dar la vuelta a la esquina a gran velocidad puesto que la inercia de tu cuerpo hace que tengas que hacer un esfuerzo importante para cambiar la dirección de tu movimiento.

Cuando estás en un colectivo y arranca, si no te agarras fuertemente de algún pasamanos verás que tu cuerpo se queda en reposo mientras el colectivo gana velocidad. Esto es muy divertido, siempre que no termines sentado arriba del pasajero del asiento del fondo,

Cuando el colectivo frena, algo similar te ocurre. Tu cuerpo sigue andando hacia adelante y deberás agarrarte fuertemente para no terminar en la cabeza del chofer ni asomándote por el parabrisas (cosa nada recomendable aunque seas cabeza dura).

Los cinturones de seguridad nos protegen en caso de un impacto frontal. Los cinturones de seguridad comunes te los ajustas a tu medida y luego el largo queda fijo. En cambio los cinturones de seguridad ; inerciales se diseñaron para que puedas moverte sin que el cinturón te tironee mientras que tus movimientos son suaves. Solamente se traban en caso de que tu cuerpo siga andando hacia adelante por inercia cuando el automóvil se detuvo bruscamente. Si el automóvil no se detiene bruscamente o tú te has atajado con las manos para no seguir andando por inercia, el cinturón no accionará su traba. Para probar si el cinturón inercial está en buen funcionamiento, tira fuertemente de él como lo haría tu cuerpo durante la frenada o choque al seguir andando por inercia a la velocidad que traía el auto anteriormente. Si el cinturón inercial se traba con un tiròn rápido, funciona correctamente; si no se traba, debe cambiarlo, ya que en esas condiciones no es un cinturón seguridad inercial sino un cinturón de adorno.

Por definiciòn se dice: "Que la inercia es la tendencia a mantener el estado de movimiento o reposo que posee un cuerpo"

Hay una resistencia natural de los cuerpos que se oponen a cambiar su estado de movimiento. Esta resistencia al cambio de estado de movimiento se llama inercia.

inercia = resistencia de un objeto a cambiar su estado de movimiento

Esta idea de Newton fue muy novedosa en su época, ya que se oponía a las concepciones que estaban de moda. Como decíamos mas arriba, antes de Newton se pensaba que todos los cuerpos tenían una tendencia natural al estado de reposo. Se creía que los objetos que se movían iban a detener su movimiento y que era necesario “hacerles algo” para mantenerlos en movimiento, pero que si se los dejaba libres de cualquier tipo de interacción, llegaban al reposo. Se creía, entonces, que había una tendencia natural de los cuerpos a alcanzar su estado de reposo.

Galileo Galilei (antes que Newton) desarrolló el concepto de inercia. Razonó que los cuerpos detenían su movimiento por una interacción de los cuerpos con su entorno, lo cual llamó fricción.

Para establecer y demostrar sus razonamientos, realizó experiencias usando dos planos inclinados enfrentados y dejando caer una pelota desde uno de ellos. Galileo observó que sí una pelota rodaba hacia abajo desde una determinada altura, alcanzaba en el otro plano una altura similar a la inicial, y que cuanto más pulidos eran los planos, más cercana era la altura alcanzada con respecto a la inicial. Galileo dedujo que la diferencia de altura observada se debía a la interacción de fricción de los cuerpos con la superficie del plano y que si esta no existiera, alcanzarían la misma altura.

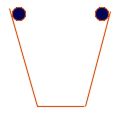
Más adelante, concluyó que, independientemente de las orientaciones de los planos, los objetos alcanzaban la misma altura.



Resumiendo: si no hay fricción alcanza la misma altura y el ángulo se reduce, recorrerá más distancia hasta alcanzar la misma altura

¿Qué sucede si el segundo plano no está inclinado?



Galileo concluyó diciendo que si el segundo plano no está inclinado, la pelota seguirá rodando sin cesar, buscando alcanzar la misma altura. Si no hubiera fricción, la pelota no se detiene nunca, sigue rodando y rodando...
Newton construyo sus ideas con los pensamientos de Galileo acerca del movimiento. La primera ley de Newton establece que no es necesaria ninguna interacción para mantener un cuerpo en movimiento. Si deslizamos un libro sobre la mesa, vemos que después de un tiempo este se detiene, pero se detiene porque existe una interacción (que es la de la fricción entre el libro y la mesa) que se opone al movimiento, y no es la ausencia de la interacción lo que lo lleva al reposo.
Todos los objetos resisten al cambio del estado de movimiento. Todos los objetos tienen esa tendencia, todos tienen inercia. Pero aquí cabe una pregunta: ¿Tienen todos los objetos la misma tendencia a resistir el cambio? La respuesta es, obviamente, ¡No! Todos tienen inercia, pero la inercia de un cuerpo depende de la masa, es decir, de la cantidad de materia que posee un cuerpo. A mayor cantidad de masa, mayor inercia y mayor resistencia al cambio del estado de movimiento. Pero esto es para la próxima clase.-

Bienvenidos al blog de Fisica de la ENET 1

Bienvenidos y mucha suerte para este año lectivo.
En este espacio virtual compartiremos las clases teóricas, las cuales estarán acompañadas de ejemplos  para comprender y aprender los temas específicos.
Para la inscripción en las clases, seleccione el curso al cual asiste y por favor, complete el formulario


Tercer Año - 1º Div

Tercer Año - 3º Div

Tercer Año - 4º Div